What is Recursion in Programming?

In this article, we will discuss the concept of recursion in programming. We will look at its usage in various programming languages, how it can be used to solve problems, its advantages and disadvantages, and many other things.

    Table Of Contents

  1. What is Recursion?
    1. Need Of Recursion
    2. Properties Of Recursion
  2. How Recursion is Used in Programming
    1. Base Condition
    2. Memory Usage
  3. Direct and Indirect Recursion
  4. Tail and Non-Tail Recursion
  5. Recursion vs Iteration
  6. Examples of Recursion
  7. Conclusion

What is Recursion?

Recursion is a process of repeating a process until a condition is met. In programming, the process is repeated in form of a function call.

So in the programming context recursion is a process in which a function is called itself until a condition is met.

These functions are called recursive functions.

Need Of Recursion

Recursion is used to solve problems that can be solved by repeated calls to the same function. It breaks down a problem into smaller sub-problems and then solves each of those sub-problems recursively.

Any problem that can be broken down into smaller sub-problems can be solved by recursion.

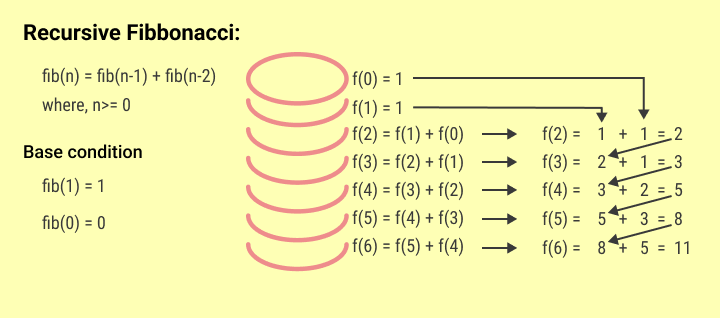
For example, if we have a problem of finding fibbonacci series, write it as fib(n) = fib(n-1) + fib(n-2), where fib(n) is the function that returns the fibbonacci series.

Properties Of Recursion

Recursion has the following properties:

  1. It performs the same task over and over again until a condition is met.
  2. Every time the function is called recursively, it has to be called with a smaller set of inputs.
  3. There must be a base case that is used to stop the recursion.

How Recursion is Used in Programming

Recursion is implemented in programming languages using functions. In programming languages, a function is a block of code that is used to perform a specific task.

Any programming language like C, C++, Java, Python, etc. can use functions and implement the concept of recursion.

We have to be very careful while writing recursive functions in programming languages. Make sure that the base case is written properly otherwise it will cause infinite recursion.

Base Condition

In every recursive function, there is a base condition that is used to stop the recursion. At the base condition, the function must return a value that is needed to solve the previous function call.

The solution is passed up in the call stack from the base condition to the previous function call and at the end, we have the final solution.

Recursion in Programming
Recursion in Programming

Memory Usage

When the main function of a program is called, the memory is allocated for the function on the call stack. The memory is deallocated when the function returns.

In the case of recursion, when the function is called recursively, the new function is allocated on the top of the call stack. And same happens again and again until the base condition is met.

Once we reach the base condition, the memory starts to deallocate from the top of the call stack as we get the return value of the function.

The memory usage of recursion is O(n) where n is the number of times the function is called.

  • Java
  • Python
#include <iostream>
using namespace std;

int fib(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fib(n-1) + fib(n-2);
    }
}

int main() {
    int n;
    cin >> n;
    cout << fib(n);
    return 0;
}
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        System.out.println(fib(n));
    }

    public static int fib(int n) {
        if (n == 0) {
            return 0;
        } else if (n == 1) {
            return 1;
        } else {
            return fib(n-1) + fib(n-2);
        }
    }
}
def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)
        
n = int(input())
print(fib(n))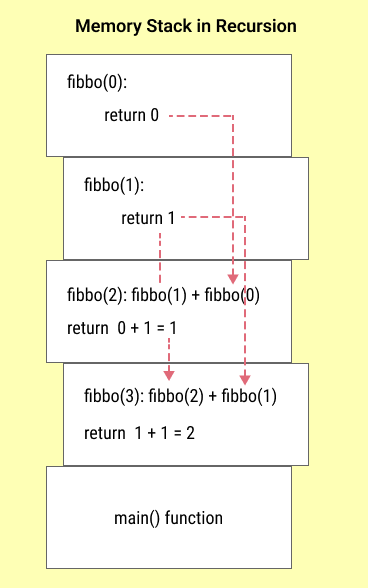
Memory Stack in Recursion
Memory Stack in Recursion

Direct And Indirect Recursion

These recursive functions can be of two types:

  1. Direct Recursive Function
  2. Indirect Recursive Function

A direct Recursive Function is a function that calls itself directly, without any other function calling it. Whereas an Indirect Recursive Function is a function that calls another function that calls itself making it an indirect recursive function.

Here is a simple example to show the difference between direct and indirect recursion.

// direct recursion
function direct() {
    // code...
    // ...

    // directly calls itself
    direct();
}

// indirect recursion
function indirect() {
    // code...
    // ...

    // call some other function that calls It
    other();
}

function other() {
    // call indirect
    indirect();
}

Tail and Non-Tail Recursion

Tail recursion is a recursive function that is called at the end of the function call. Non-Tail recursion is a recursive function that is called at the beginning of the function call.

You may be thinking why does it matter where the recursive call is made?🤔

The reason is tail recursion is better than non-tail recursion. Because we know recursive function creates a stack when the recursive function call is the last statement in the function, then there is no need to store its address in the stack and it is popped off the stack making it faster.

Examples of Recursion

Here are some examples of recursion.

Factorial

The factorial of a number is the product of all the numbers from 1 to that number. For example, the factorial of 5 is 5 * 4 * 3 * 2 * 1 = 120.

Here is the program to find the factorial of a number using recursion.

  • Java
  • Python
#include <iostream>
using namespace std;

int factorial(int n) {
    if (n == 0) {
        return 1;
    } else {
        return n * factorial(n-1);
    }
}

int main() {
    int n;
    cout << "Enter a number: ";
    cin >> n;
    cout << factorial(n);

    return 0;
}
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.println("Enter a number: ");
        int n = sc.nextInt();
        System.out.println(factorial(n));
    }
    public static int factorial(int n) {
        if (n == 0) {
            return 1;
        } else {
            return n * factorial(n-1);
        }
    }
}
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

n = int(input("Enter a number: "))
print(factorial(n))

Output:

Enter a number: 5
120

Binary search is a search algorithm that works by comparing the value of the middle element of the array with the value being searched for. If the value is less than the middle element, then the search continues on the lower half of the array. If the value is greater than the middle element, then the search continues on the upper half of the array. This continues until the value is found or the search ends.

The binary search algorithm uses recursion to search for the value in the array.

Here is the program for this.

  • Java
  • Python
#include <iostream>
using namespace std;

int binarySearch(int arr[], int l, int r, int x) {
    if (r >= l) {
        int mid = l + (r - l) / 2;
        if (arr[mid] == x) {
            return mid;
        } else if (arr[mid] > x) {
            return binarySearch(arr, l, mid - 1, x);
        } else {
            return binarySearch(arr, mid + 1, r, x);
        }
    } else {
        return -1;
    }
}

int main() {
    int arr[] = {2, 3, 4, 10, 40};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    if (result == -1) {
        cout << "Element not found";
    } else {
        cout << "Element found at index " << result;
    }
    return 0;
}
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int arr[] = {2, 3, 4, 10, 40};
        int n = arr.length;
        int x = 10;
        int result = binarySearch(arr, 0, n - 1, x);
        if (result == -1) {
            System.out.println("Element not found");
        } else {
            System.out.println("Element found at index " + result);
        }
    }
    public static int binarySearch(int arr[], int l, int r, int x) {
        if (r >= l) {
            int mid = l + (r - l) / 2;
            if (arr[mid] == x) {
                return mid;
            } else if (arr[mid] > x) {
                return binarySearch(arr, l, mid - 1, x);
            } else {
                return binarySearch(arr, mid + 1, r, x);
            }
        } else {
            return -1;
        }
    }
}
def binarySearch(arr, l, r, x):
    if r >= l:
        mid = l + (r - l) / 2
        if arr[mid] == x:
            return mid
        elif arr[mid] > x:
            return binarySearch(arr, l, mid - 1, x)
        else:
            return binarySearch(arr, mid + 1, r, x)
    else:
        return -1

arr = [2, 3, 4, 10, 40]
x = 10
result = binarySearch(arr, 0, len(arr) - 1, x)
if result == -1:
    print("Element not found")
else:
    print("Element found at index " + str(result))

Output:

Element found at index 3