Standard Deviation: Explained with Examples
The standard deviation is an important statistical term that plays a key role in the study of statistical and mathematical analysis. The concept of the standard deviation is very useful for analyzing the variation of the data sets from the mean or average of the given data. The standard deviation elaborates on the sort or type of data distribution.
The objective of determining the variation or scattering of the data points is to analyze the behavior of each and every entity or unit of the population about the mean value. It enables us to apprehend the relation of two data sets and compare them precisely.
In this article, we'll explore the definition, formulas, and method to evaluate standard deviation along with solved examples.
Definition
The standard deviation of a given data set can be defined as the + ve square root of the mean of the squared deviations of kth observations (i = 1, 2, 3, …, k) from their arithmetic mean (A.M). The standard deviation elaborates on the evaluation or the measurement of the data spread about the average of the given data values.
Formula
Mathematically, the standard deviation for the population is defined as:
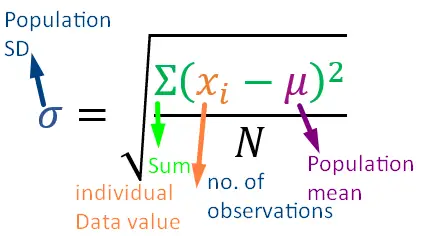
Here it is important to elaborate on that in the formula of standard deviation for the sample data N is replaced by (n – 1) and the mu symbol by x̄. The notation used for the sample's SD is Sx. Mathematically,
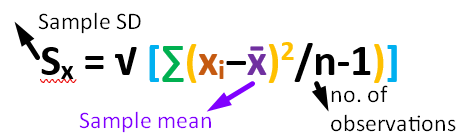
It can be concluded by observing the mathematical formula the standard deviation can never be negative because in the mathematical formula square of the (x - x̅)2 values. If the SD is small, it elaborates that data values lie near the mean value.
How to find standard deviation?
It is essential to understand how to find standard deviation from the given data. Here we will explain how to find SD from the given data values.
- First of all, determine the mean of the data values which is equivalent to the sum of the observations over the total number of observations i.e. µ = ∑ x/n
- Find the difference (x - µ) for each data value.
- Determine the square of all data values obtained in the preceded step i.e. (x - µ)2.
- Now determine the sum of all the data values i.e. ∑(x - µ) 2 .
- For population SD divide ∑(x - µ)2 by the total number of observations i.e. ∑(x− µ)2/n but for sample SD divide this obtained value by (n – 1) and take the square root of this value that will be the required answer.
Examples
Now let us see some examples to comprehend the term standard deviation precisely.
Example 1:
The marks of six students in economics are given in the following table:
| Student No. | 1 | 2 | 3 | 4 | 5 | 6 |
| Marks | 54 | 90 | 40 | 63 | 84 | 47 |
What will be its standard deviation.
Solution:
Step 1: Given information:
Marks of students in arranged form: 40, 47, 54, 63, 84, 90
Step 2: First of all, find the mean of the data values.
µ = (40 + 47 + 54 + 63 + 84 + 90) / 6
µ = 378/6 = 63
Step 3: Suppose x = student's marks. We will compute SD following the given computations:
| x | (x - µ) | (x - µ)2 |
| 40 | -23 | 529 |
| 47 | -16 | 256 |
| 54 | -9 | 81 |
| 63 | 0 | 0 |
| 84 | 21 | 441 |
| 90 | 27 | 729 |
| ∑(x - µ)2 = 2036 |
Step 4: Putting the relevant values in the formula:
σ = √ [∑ (x − µ)2 / N] σ = √(2036/6) σ = 18.42 Ans.
Example 2:
What will be the standard deviation for the given sample data
7, 4, 2, 8, 6, 3, 2, 5, 1, 1, 2, 7
Solution:
Step 1: Given information in arranged from:
7, 4, 2, 8, 6, 3, 2, 5, 1, 1, 2, 7
Step 2: The mean value for the given information:
x̄ = (7+ 4 + 2 + 8 + 6 + 3 + 2 + 5 + 1 + 1 + 2 + 7) / 12 x̄ = 48 / 12 x̄ = 4
Step 3: Suppose x = data value, we will compute SD following the given computations:
| x | (x - x̄) | (x - x̄)2 |
| 7 | 3 | 9 |
| 4 | 0 | 0 |
| 2 | -2 | 4 |
| 8 | 4 | 16 |
| 6 | 2 | 4 |
| 3 | -1 | 1 |
| 2 | -2 | 4 |
| 5 | 1 | 1 |
| 1 | -3 | 9 |
| 1 | -3 | 9 |
| 2 | -2 | 4 |
| 7 | 3 | 9 |
| ∑(x - x̄)2 = 70 |
Step 4: Putting the relevant values.
S = √ (∑x−x̄) 2 /(n-1) S = √ [70 / (12 – 1)] S = √ (70 / 11) S = 2.52 Ans.
Example 3:
What will be the standard deviation for the given observations?
23, 35, 41, 56, 67, 78
Solution:
Step 1: Given information in arranged form:
23, 35, 41, 56, 67, 78
Step 2: For mean:
µ = x̄ = (23 + 35 + 41 + 56 + 67 + 78) / 6 µ = x̄ = 300 / 6 µ = x̄ = 50
Step 3: Suppose x = data value, we will compute SD following the given computations:
| x | (x - µ) = (x - x̄) | (x - µ)2 = (x - x̄)2 |
| 23 | -27 | 729 |
| 35 | -15 | 225 |
| 41 | -9 | 81 |
| 56 | 6 | 36 |
| 67 | 17 | 289 |
| 78 | 28 | 784 |
| ∑(x - µ)2 = ∑(x - x̄)2 = 2144 |
Step 4: Formula:
For Population SD:
σ = √(∑(x− µ)2 /n)
Place the relevant values in the formula:
σ = √ (2144/6) σ = √(364.48) σ = 19.09
For sample SD:
S = √ ∑(x−x̄) 2 /(n-1)
Place the relevant values in the formula:
S = √[2144/(6-1)] S = √(2144/5) S = √(428.8) S = 20.71 Ans.
Wrap Up
In this article, we have elaborated on the statistical term standard deviation. We have explored its definition, mathematical formula, and significant method that is useful to determine the SD for both sample and population data values. We also solved some examples to apprehend the important calculations to compute SD.
