Boolean Algebra: An Introduction to its Definition, Operations, and Applications
Boolean algebra is a frequently used topic in digital circuits, mathematics, computer science, etc. Boolean algebra uses binary variables for representing true and false such as 0 for false and 1 for true. There are different operations of Boolean algebra used on a wider scale for various purposes.
In this article, we'll explore the basic definition, operations of Boolean algebra, and applications with examples.
What is Boolean algebra?
The term Boolean algebra was developed in the mid of the 19 th century by George Boole. Boolean algebra is a fundamental branch of algebra that is frequently used to study the manipulation of logical expressions as well as logic gates.
Boolean algebra deals with only two terms either true or false. For the representation of true and false, Boolean algebra uses binary numbers 0 and 1. The binary number 0 is used to represent a false statement while the binary number 1 is used to represent a true statement.
The study of Boolean algebra is very essential in those fields where logical operations have great importance. It is very useful for understanding the working of computers and provides full guidance for analyzing and designing digital circuits.
Operations of Boolean algebra
To manipulate the Boolean expressions, Boolean algebra uses various operations such as:
- AND
- OR
- NOT
- XOR
- NAND
- NOR
- XNOR
The explanation of these operations is given below.
| Operations | Explanation |
|---|---|
| AND | AND operation also known as AND gate is the multiplication operation of Boolean algebra. It is denoted by the symbol hat “∧” or dot “.” To represent the product. The logical conjunction is another name for the AND operation. It takes two input values such as (0 ∧ 0), (0 ∧ 1), (1 ∧ 0), and (1 ∧ 1), and produces an output that is true (1) only if both inputs are true (1 ∧ 1). |
| OR | OR operation also known as OR gate is the addition operation of Boolean algebra. It is denoted by the symbol “∨” or “+”. The logical disjunction is another name for OR operation. It takes two input values such as (0 ∨ 0), (0 ∨ 1), (1 ∨ 0), and (1 ∨ 1), and produces an output that is true (1) if at least one input is true (1) and false when both the inputs are false (0 ∨ 0) |
| NOT | NOT operation also known as NOT gate is the inversion operation of Boolean algebra. It is denoted by the symbol “¬” or “~”. The logical negation is another name for NOT operation. It takes a single input value such as 0 or 1 and produces an output that is the opposite of the input value such as 1 or 0. For example, if the input is false (0), the output is true (1), and vice versa. |
| XOR | XOR operation also known as XOR gate is the advanced form of OR gate. It is denoted by the symbol “⊕” and stands for exclusive or. It takes two input values and produces an output that is true (1) if the inputs are different such as (0 ⊕ 1) & (1 ⊕ 0), and false (0) if they are the same such as (0 ⊕ 0) & (1 ⊕ 1). |
| NAND | NAND operation also known as NAND gate is the opposite of AND operation. It is denoted by the symbol “↑” or “|¬”. It inverts the results of the AND operation. It takes two input values such as (0 ¬ 0), (0 ¬ 1), (1 ¬ 0), and (1 ¬ 1), and produces an output that is false (1) only if both inputs are true (1 ∧ 1). |
| NOR | NOR operation also known as NOR gate is the opposite of OR operation. It is denoted by the symbol “↓” or “|~”. It inverts the results of the OR operation. It takes two input values such as (0 ↓ 0), (0 ↓ 1), (1 ↓ 0), and (1 ↓ 1), and produces an output that is false (0) if at least one input is true (1) and true when both the inputs are false (0 ↓ 0) |
| XNOR | XNOR operation also known as XNOR gate is the opposite of NOR operation It is denoted by the symbol “≡” or “⊙”. It inverts the results of the XOR operation. It takes two input values and produces an output that is false (0) if the inputs are different such as (0 ≡ 1) & (1 ≡ 0), and true (1) if they are the same such as (0 ≡ 0) & (1 ≡ 1). |
Applications of Boolean algebra
Boolean algebra is used in different fields such as:
- Mathematics
- Telecommunication
- Digital Circuits
- Computer Science
- Artificial Intelligence
Here is the explanation of the above mentioned applications of Boolean algebra.
| Applications | Explanation |
|---|---|
| Mathematics | In mathematics, Boolean algebra is used to study abstract structures such as Boolean rings and lattices. It is also used in set theory to study the properties of sets and their relationships. |
| Telecommunication | In telecommunications, Boolean algebra is helpful for designing and analyzing the communication network. It is used to optimize network performance and minimize transmission errors. |
| Digital Circuits | For the analysis and design of digital circuits, Boolean algebra is used widely. The Boolean algebra logic gates (operations) are very essential for the implementation of various functions in the digital circuit such as memory. |
| Computer Science | In computer science, logical operations can be represented and manipulated with the help of Boolean algebra. The uses of Boolean algebra in computer science are:
|
| Artificial Intelligence | In artificial intelligence, Boolean algebra is used to represent and manipulate knowledge. It is used in expert systems to represent rules and in neural networks to model complex relationships between inputs and outputs. |
Examples of Boolean algebra
Here are a few examples of Boolean algebra evaluated with the help of truth tables.
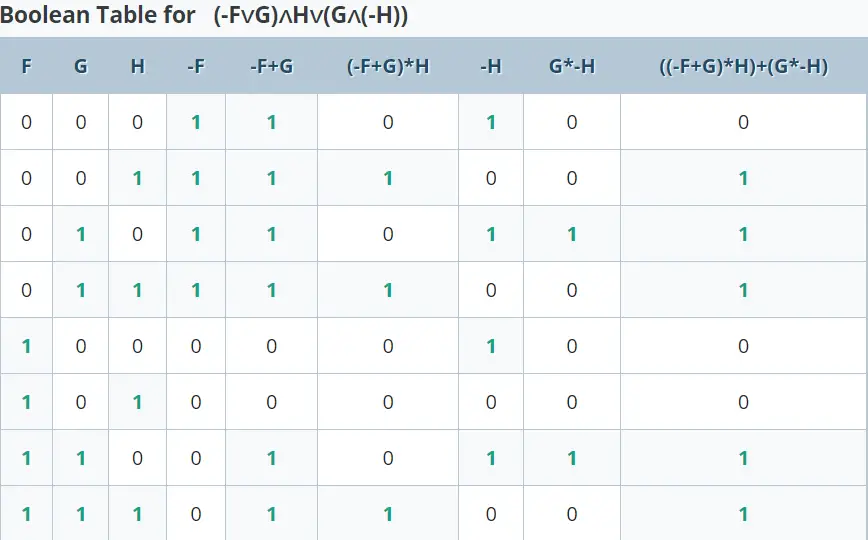
Example 1
Solve the given expression with the help of the truth table.
(¬F ∨ G) ∧ H ∨ (G ∧ ¬H) + F
Step 1: There will be 8 rows in the truth table as 3 variables (F, G, & H) are available in the expression. First, write the negation values of F and H.
After that solve the brackets terms.
| F | G | H | ¬F | ¬H | ¬F ∨ G | G ∧ ¬H | (¬F ∨ G) ∧ H | (¬F ∨ G) ∧ H ∨ (G ∧ ¬H) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
A boolean expression calculator can be used to solve the problems of binary algebra with the help of a truth table.
Example 2
Solve the given expression with the help of the truth table.
(F . G) H + F[¬F + (H + ¬G)]
Step 1: There will be 8 rows in the truth table as 3 variables (F, G, & H) are available in the expression. First, write the negation values of F and G.
After that solve the brackets terms.
| F | G | H | ¬F | ¬G | F . G | (F . G) H | H + ¬G | ¬F + (H + ¬G) | F[¬F + (H + ¬G)] | (F . G) H + F[¬F + (H + ¬G)] |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Final Words
Boolean algebra is one of the main types of algebra that deals with the logic gates and operations to manipulate Boolean expressions. The applications of Boolean algebra are vast as it is used in various fields.
